计数与二进制--------------李铁圣(香港)高五组【校友文萃】
|
计数与二进制 三字经中有“一而十、十而百、百而千、千而万”之句。初看起来,这仅是小学生最基本的算数而已。然而这些简单的数数却有着高深之学问。 人类之初,人们是怎样进行计数的呢?有一种说法是,因为人有十个指头,因而发明了一到十的计数。另一种说法是,古老时代人们将绳子打结,打一个结代表一只羊,后来结绳已不够用,于是发明一到十、百、千、万之数目字了。由此可见,一者为数之始,十者为数之终。十个十成一百,十个百成一千,十个千成一万,这就是我们所熟悉的十进制计数。大家知道,宇宙之形成是由无极生太极,太极生两仪发展来的,所谓太极者亦为天地未分之前,元气混而为一,故一者为天地阴阳之始,也是为数之始也! 随着历史的演变,科学技术不断取得进步,计算事物的方法愈来愈快,愈来愈精确,单纯的数数已不能满足事物演进的需求,于是人类又发明了加减乘除等等的计算方法,算数这门学问就越来越深奥了。时至今日,人类的文明经过一级又一级的演进,现在已经到了资讯化的时代,一个国家的资讯化程度已成为衡量它的进步与实力的重要指标,人类将走入一个无处不资讯的社会了。资讯化的时代最典型的事例是超大型集成电路——第四代电脑的出现。 由于电脑所使用的数字系统并非我们所熟悉的十进制系统,而是采用一种叫二进制的系统。这个系统只由0与1两个数字所组成,在进行运算时,作业速度非常快,储存容量非常大,而处理结果正确性又非常高,同时它具有电位传输能力,可以超越空间限制。 那么,二进制这个概念又是如何产生的呢?大家知道,十进制中,计数时逢十进一,例9+1=10,99+1=100,1+1=2,人们发现,一根筷子加一根筷子可以是两根筷子,但说成一对筷子也未尝不可,这样就产生1+1=1之概念,事实上,这种概念又源于太极生两仪之说,太极经无数组合,得到规律,产生互相对立的两仪现象,如天与地、阴与阳、对与错、正与负、黑与白、开与关等等。之后,天体出现,运行开始,一切进入生死循环之运行轨道。两仪现象给人们一个启示,自然中的一切事物可否用两仪中的两个对立面来窥见事物的全貌呢?研究结果其结论是肯定的。现在,我们不妨将事物的两个对立面中一个用“1”表示,一个用“0”表示。例如,当我们想知道灯泡在亮时和不亮时其电压与波形之间的关系时,不妨将亮时假设为“1”,暗时假设为“0”,这样就不难得到如下的图形:
可见用二进制表示,灯泡亮与不亮时其电压与波形之间的关系可一目了然。 那么,我们通常所习惯的十进制与二进制之间之表示方法如何进行转换呢?大家很清楚,在十进投影中任何一个数值,其数字在各个不同的位置时其数值都不同,例数值32767,各数字处于不同位置,所代表之数值都不同的,第一位7,表示有七个1(
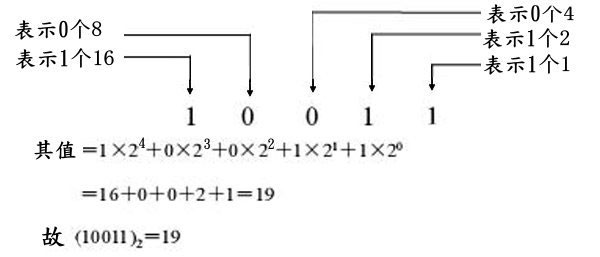
同理,在二进制中,由于只能用“1”和“0”两个数字,所以其值在不同位置时所表示的应为
现在,让我们谈谈如何将十进制和二进制互转。 一. 十进制数值写为二进制数值 只要将十进制的数据连续除以2,并将其最后的商及余数连起即可,例十进制中的100,写成二进制应是
(2) 后小数部分:
二. 二进制中的数值写成十进制的数值 例二进制的 (111)2,写成十进制应是 1× 则 (111)2=7 1× =64+0+0+8+0+0+0=72 则 (1001000)2=72 (1111.11)2=1× =8+4+2+1+0.5+0.25=15.75
第五代计算机的二进制系统采用的是光通信技术,其运用的空间无限广阔,可处理声音,人工智能,能够积累知识,可以自行推理等。 |

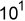 );
);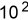 );
);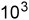 );第五位3,表示有三个10000(
);第五位3,表示有三个10000(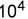 )。
)。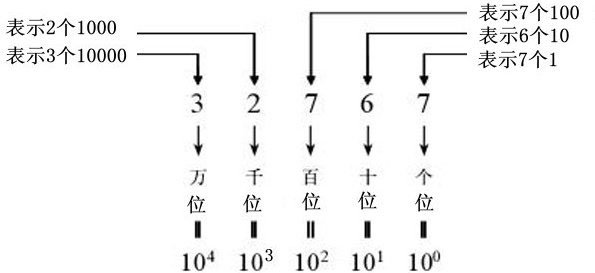
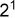 ,第三位表示为0个
,第三位表示为0个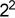 ,第四位表示为0个
,第四位表示为0个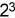 ,第五位表示为1个
,第五位表示为1个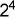 。
。
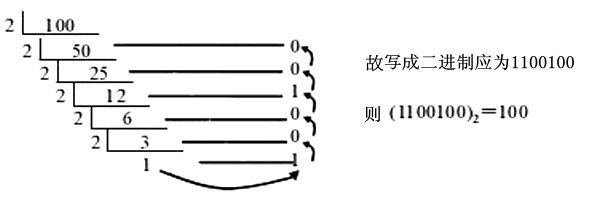

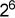 +0×
+0×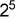 +0×
+0×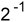 +1×
+1×